Optimiser pour se remettre des perturbations dans l'industrie du transport maritime par conteneurs

Le transport maritime est une industrie complexe qui lie les fournisseurs et leurs clients dans le monde entier grâce au transport de conteneurs sur un réseau de distribution hautement optimisé. Ces entreprises exploitent des réseaux de transport de marchandises d'un point à l'autre du globe, en utilisant des navires de grande capacité appelés porte-conteneurs. Dans les années 1960, l'innovation de la conteneurisation a eu un impact considérable sur l'industrie et a révolutionné le marché de l'import-export de marchandises en réduisant drastiquement les coûts, grâce à l'augmentation du nombre de marchandises transportées par voyage.

Aujourd'hui, la quasi-totalité du commerce maritime s'effectue de cette manière et il est donc évident que des solutions numérisées associées à la modélisation mathématique émergent et se concentrent principalement sur cet aspect, car les gains économiques et environnementaux sont facilement obtenus et mesurables.

Tout d'abord, ce système de transport exige que les marchandises soient regroupées dans des conteneurs et chargées sur des navires de grande capacité. Ensuite, les navires et les conteneurs voyagent sur un réseau de routes maritimes exploitées par des compagnies maritimes et des ports commerciaux. Dans la plupart des cas, le voyage d'un conteneur de son point d'origine à sa destination consiste en plusieurs navires consécutifs lui permettant d'atteindre le point de livraison final. Le processus de chargement et de déchargement des conteneurs d'un navire à l'autre est connu sous le nom de transbordement.

L'un des problèmes les plus critiques auxquels les compagnies maritimes sont confrontées quotidiennement et qui n'a jamais été automatisé auparavant est la gestion de la récupération des perturbations imprévisibles. Cela génère un grand nombre de coûts opérationnels supplémentaires. Une perturbation imprévisible se produit lorsqu'un ou plusieurs navires sont retardés. Ces événements perturbateurs sont très difficiles à prévoir à long terme (grèves, tempêtes, pannes, etc.), ce qui entraîne des écarts importants par rapport à la planification du réseau opérationnel. Non seulement le navire retardé est concerné, mais un nombre important de navires adjacents dans le réseau sont également affectés par l'effet domino, résultant des transbordements retardés dans les ports à la suite de la perturbation. Le respect des délais de livraison de ces marchandises est donc directement affecté et représente une menace pour la société en termes de satisfaction des clients et de perte de parts de marché au profit de concurrents plus ponctuels.

Il peut être difficile pour un œil humain d'identifier, dans un court délai, la meilleure solution compte tenu de la complexité du réseau en place. Plus l'opérateur attend pour prendre une décision, moins il reste de possibilités et plus les coûts de rattrapage sont élevés. Il est crucial pour l'opérateur de transport de prendre des mesures rapides pour limiter les dommages causés à ses services par ces interruptions de service. C'est là que la recherche opérationnelle, également connue sous le nom d'optimisation mathématique, entre en jeu. La modélisation en réseau des actions de rétablissement potentielles dans une structure de graphe permet aux opérateurs de s'appuyer sur un outil mathématique non subjectif qui donne des résultats quantifiés dans un court laps de temps. Cet article présente le modèle mathématique développé et appliqué aux cas pratiques pour aider la compagnie maritime à se remettre des perturbations imprévisibles qui affectent son réseau.

Il existe plusieurs solutions pour limiter l'impact de l'interruption du service, comme le raccourcissement du temps d'accostage ou même l'insertion d'un navire inactif attendant à quai pour récupérer les conteneurs en attente, mais les solutions les plus courantes sont les suivantes, et ce sont elles que le modèle prendra en considération :

• Accélérer le navire : Le navire se déplaçant à une vitesse bien inférieure à sa vitesse maximale, l'accélération est un moyen efficace de respecter le calendrier. Toutefois, cette solution est très onéreuse, surtout lorsque le navire parcourt de longues distances, en raison des coûts importants liés à la consommation de carburant.
• Sauter une escale : Lorsqu'un navire subit une perturbation majeure, une décision radicale peut être prise : ne pas faire d'escale. Cela permet un rétablissement rapide, mais au prix de retards et de mauvaises connexions des conteneurs qui devaient transiter par le port omis.
• Échanger les escales : cette mesure n'est pertinente que lorsque les ports sont relativement proches l'un de l'autre et que le deuxième port inscrit au calendrier est plus important en termes de livraisons de conteneurs que le précédent. Elle est souvent utilisée pour s'assurer que les grandes expéditions sont livrées à temps. Cela a un impact significatif sur le retard du premier port, mais garantit la livraison à temps des cargaisons plus importantes au second port et minimise ainsi l'impact sur un plus grand nombre de clients.

Le modèle doit prendre en compte la dimension spatiale (un navire naviguant entre différents ports pour livrer ses marchandises) et temporelle (horaire à respecter sous peine de manquer sa connexion à un conteneur) du problème.

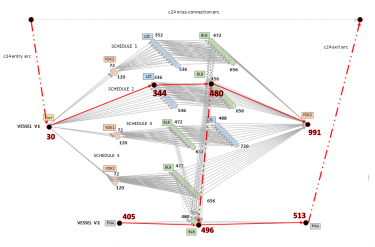
La première façon de modéliser le problème est de le considérer comme un graphe et de considérer les navires, les conteneurs et les ports comme des objets définissant ce graphe. Chaque nœud du graphe est défini comme la position possible d'un navire, dans un port donné, à un moment donné. Chaque arc représente alors un trajet possible entre deux escales (position dans un port à un moment donné) à une vitesse donnée.

Un tel problème de perturbation soulève la question suivante : comment récupérer une perturbation et ramener tous les navires au programme initial tout en réduisant les coûts opérationnels et en respectant les contraintes physiques. Tout d'abord, un cadre doit être établi, chaque retard affectant un navire spécifique inclut un sous-ensemble de navires adjacents susceptibles d'être affectés par la perturbation. Ces navires adjacents sont censés prendre en charge le transbordement des conteneurs retardés après la perturbation. Le champ d'application est ensuite défini géographiquement autour des navires concernés, de leurs positions et de leurs itinéraires possibles, et enfin par un horizon temporel défini obligeant les navires à se rétablir avant une certaine date limite fixe. (À titre d'exemple, il existe un calendrier de passage groupé obligatoire pour les navires de nombreuses sociétés passant par le canal de Suez afin de réduire les coûts fiscaux). Ce cadre délimite la complexité et réduit la taille du modèle à ce qui est réellement affecté par les perturbations.

Le modèle est donc basé sur un graphe temporel orienté où les nœuds sont associés à un triplet (navire, port, heure) et les arcs définissent les segments réalisables de toutes les routes potentielles des navires à travers le réseau selon le scénario de reprise.

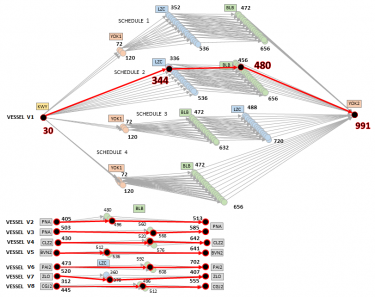
Note au lecteur : dans cette configuration, le choix a été fait de dupliquer certains nœuds avec différents scénarios (dans la figure 1, le nœud (V1,LZC,352) par exemple existe pour les scénarios 1 et 2, et le nœud (V1,LZC,536) pour les scénarios 1,2 et 3). Ce choix est discutable en raison de l'augmentation du nombre de variables à prendre en compte par le modèle mathématique par la suite, mais il permet également de ne pas imposer de contrainte de scénario au sein du modèle puisqu'aucun arc ne relie les nœuds aux différents scénarios. Cela réduit considérablement le nombre de contraintes à prendre en compte. C'est cette deuxième option qui a été privilégiée dans la définition du graphique.

Après la définition du réseau graphique, l'étape la plus importante consiste à déterminer les coûts et donc la fonction objective du problème que le modèle cherchera à minimiser. L'idée d'utiliser la recherche opérationnelle est d'aider à résoudre un problème complexe de prise de décision entre les principaux coûts impliqués :

• Coûts de consommation de carburant : tous les coûts liés à la consommation de carburant (accélération). Ils représentent 25 % des coûts d'exploitation totaux des grandes compagnies maritimes.
• Pénalité pour les conteneurs retardés : Lorsqu'un groupe de conteneurs est retardé, la compagnie maritime subit une perte de satisfaction du client. Cette perte est représentée dans le modèle par une pénalité financière fictive. Cette pénalité dépend linéairement du nombre de conteneurs retardés. Il s'agit d'un coût stratégique intégré dans la fonction objective qui indique le montant que la compagnie est prête à payer pour éviter que les conteneurs ne soient retardés.
• Pénalité pour les conteneurs qui ont manqué leur correspondance : comme précédemment, lorsqu'un groupe de conteneurs manque sa correspondance, la compagnie maritime encourt une pénalité financière fictive qui dépend linéairement du nombre de conteneurs. Lorsqu'un conteneur est mal connecté, il reçoit à la fois la pénalité pour retard et pour mauvaise connexion.

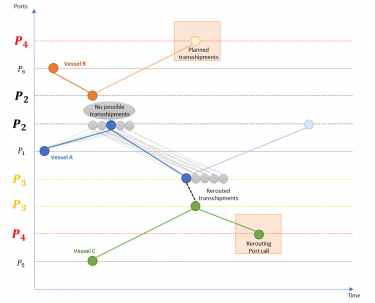
Ce modèle présente de bons résultats et a prouvé son efficacité dans de nombreux cas concrets où le modèle fournit une solution au moins aussi bonne que celle adoptée par les opérateurs lorsque la situation s'est produite directement. Cependant, il présente de nombreuses lacunes, dont la plus évidente concerne la récupération des conteneurs qui ont été retardés ou qui ont manqué leur correspondance. En effet, le modèle actuel ne permet pas de régénérer un horaire pour les conteneurs qui ont été retardés ou déconnectés, ils sont simplement considérés comme une pénalité dans la fonction objective et disparaissent du modèle sans avoir de proposition de récupération. Il est donc évident que la modélisation graphique doit intégrer une nouvelle instance dans sa modélisation : les conteneurs.

Comme décrit ci-dessus, la fonction objective du problème modélise la somme des coûts de la solution à minimiser. Elle prend en compte les coûts de carburant et les coûts de pénalité fictifs en cas de retard ou de mauvaise connexion de la cargaison. Les instances modélisées sont soumises à des contraintes garantissant la faisabilité de la solution générée :

• Contraintes sur chaque port garantissant qu'une escale dans le programme est soit utilisée dans la solution, soit considérée comme omise ;
• Contraintes de maintien des débits sur : -chaque port : maintien du débit des bateaux passant par le quai ; -chaque navire : maintien du débit de conteneurs à bord ;
• Contraintes liées aux pénalités de retard ou de mauvaise connexion pour les conteneurs livrés ou non livrés.

Les algorithmes des deux modèles ont été exécutés pour chacun des quatre cas d'utilisation. Les solutions et les performances ont été comparées et confrontées aux décisions réelles prises par le personnel opérationnel. Tout d'abord, il convient de mentionner que les deux modèles ont fourni des solutions au moins aussi bonnes que celles choisies par les opérateurs en fonction de la situation. Pour certains, les décisions prises par les agents étaient optimales selon le modèle, pour d'autres, l'utilisation des deux modèles aurait permis de mieux conseiller les agents et d'économiser des frais de recouvrement de planning. Les deux modèles ont fourni les mêmes solutions pour les quatre cas d'utilisation puisqu'il n'y avait pas de place pour le réacheminement des cargaisons dans les deux cas d'utilisation. Afin d'évaluer la performance du nouveau modèle, la méthode de sélection des navires à inclure dans la simulation doit être repensée pour ajouter des navires capables de proposer des routes alternatives pour les conteneurs retardés et de mieux évaluer les solutions de reroutage des cargaisons.

Au cours de cette étude, un autre cas d'utilisation a été développé pour tester les avantages potentiels de l'intégration du reroutage des conteneurs. Sur la base des cas utilisés pour le premier modèle, les données ont été élargies en ajoutant des navires supplémentaires offrant des itinéraires alternatifs pour que les conteneurs atteignent leur destination finale. Les résultats ont été satisfaisants puisque le second modèle modélisant les conteneurs propose de réacheminer certains d'entre eux, alors que le premier modèle les considère simplement comme des conteneurs retardés ou non connectés. Le second modèle s'est avéré satisfaisant en proposant de meilleurs résultats que le premier, à condition qu'un réseau plus large soit pris en compte par le modèle afin que toutes les actions de récupération possibles pour les navires et les conteneurs soient pleinement évaluées. 

La recherche opérationnelle sert ici de puissant accélérateur de décision, toutes les options modélisées sont évaluées et comparées analytiquement sur la base de leurs coûts estimés et l'optimum est mis en évidence. Cette méthode reste un outil puissant de traitement des données en tenant compte des paramètres d'entrée et n'a pas vocation à remplacer les décisions d'un opérateur humain. Ce dernier peut alors évaluer plus précisément la faisabilité d'une solution théoriquement optimale proposée par l'outil et modifier itérativement les paramètres en fonction de ses observations afin de prendre la meilleure décision possible.